Найти минимальное и максимальное значение в двоичном дереве поиска
Эта серия проблем приведет к созданию структуры данных дерева. Деревья - важная и универсальная структура данных в информатике. Конечно, их имя исходит из того факта, что при визуализации они очень похожи на деревья, с которыми мы знакомы в естественном мире. Структура данных дерева начинается с одного узла, обычно называемого корнем, и отсюда разветвляется на дополнительные узлы, каждый из которых может иметь больше дочерних узлов и т. Д. И т. Д. Структура данных обычно визуализируется с корневым узлом вверху; вы можете думать об этом, как естественное дерево перевернулось вверх дном. Сначала давайте опишем некоторую общую терминологию, с которой мы столкнемся с деревьями. Корневой узел - это вершина дерева. Точки данных в дереве называются узлами. Узлы с ветвями, ведущими к другим узлам, называются родителями узла, к которому ведет ветвь (дочерний элемент). Другие более сложные семейные термины применяются, как и следовало ожидать. Поддерево относится ко всем потомкам конкретного узла, ветви могут упоминаться как ребра, а листовые узлы - узлы в конце дерева, у которых нет детей. Наконец, обратите внимание, что деревья являются по своей природе рекурсивными структурами данных. То есть, любые дочерние узлы являются родителями собственного поддерева и так далее. Рекурсивный характер деревьев важен для понимания при разработке алгоритмов для общих операций дерева. Для начала обсудим конкретный тип дерева - двоичное дерево. Фактически, мы фактически обсудим конкретное двоичное дерево, двоичное дерево поиска. Давайте опишем, что это значит. Хотя структура данных дерева может иметь любое количество ветвей в одном узле, двоичное дерево может иметь только две ветви для каждого узла. Кроме того, двоичное дерево поиска упорядочено относительно дочерних поддеревьев, так что значение каждого узла в левом поддереве меньше или равно значению родительского узла, а значение каждого узла в правом поддереве равно больше или равно значению родительского узла. Очень полезно визуализировать эти отношения, чтобы лучше понять это:
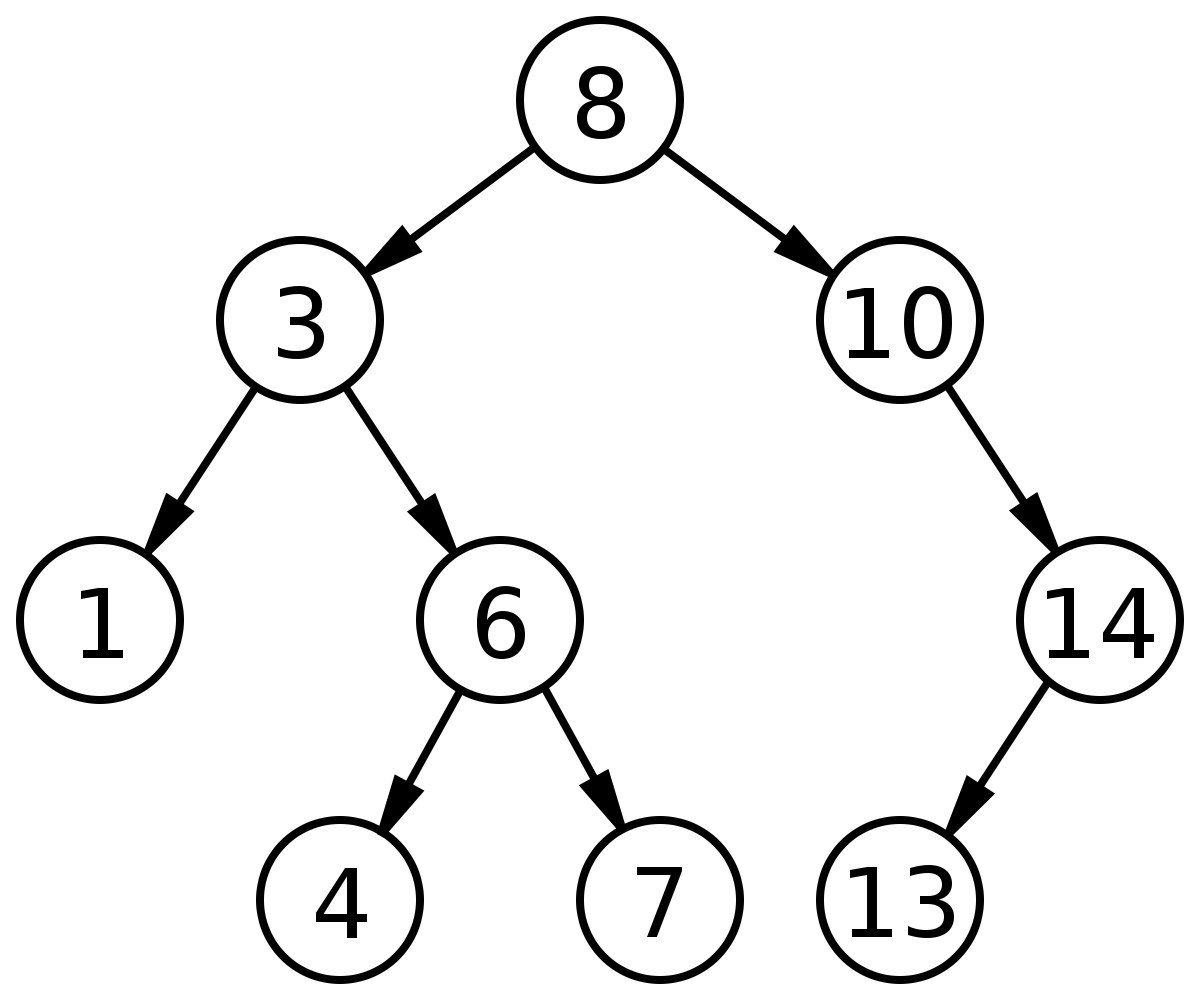
findMin и findMax . Эти методы должны возвращать минимальное и максимальное значение, хранящиеся в двоичном дереве поиска (не беспокойтесь о добавлении значений в дерево на данный момент, мы добавили некоторые в фоновом режиме). Если вы застряли, подумайте об инварианте, который должен быть истинным для двоичных деревьев поиска: каждое левое поддерево меньше или равно его родительскому элементу, и каждое правое поддерево больше или равно его родительскому. Давайте также скажем, что наше дерево может хранить только целочисленные значения. Если дерево пустое, любой метод должен возвращать значение null .We'll start simple. We've defined the skeleton of a binary search tree structure here in addition to a function to create nodes for our tree. Observe that each node may have a left and right value. These will be assigned child subtrees if they exist. In our binary search tree, define two methods, findMin and findMax. These methods should return the minimum and maximum value held in the binary search tree (don't worry about adding values to the tree for now, we have added some in the background). If you get stuck, reflect on the invariant that must be true for binary search trees: each left subtree is less than or equal to its parent and each right subtree is greater than or equal to its parent. Let's also say that our tree can only store integer values. If the tree is empty, either method should return null.